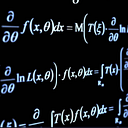Model Predictive Control (MPC) for Autonomous Vehicles
Introduction
This article discusses a Model Predictive Controller (MPC) I built as part of Udacity’s self-driving car nanodegree program (term 2). The project objective was to control a vehicle in a simulator environment to drive as fast as possible without leaving the drivable area. This work was done in the Spring of 2017 — and for more details, please refer to my GitHub repository.
An inquisitive reader may wonder why we even need a controller if we already have a reference trajectory coming from the path planner module. The reason is because the reference trajectory (from the path-planner module) is of the form position(x,y) and velocity. But we cannot directly influence them. The only “knobs” we are able to directly influence are the throttle and steering angle of the vehicle. And so the job of the controller is to adjust the throttle and steering angle such that the true position and velocity of the vehicle is as close as possible to the reference position and velocity. There are many different types of controllers ranging from simpler ones like Proportional-Integral-Derivative (PID), Linear Quadratic Regulator (LQR), etc to more sophisticated ones like MPC.
MPC is an optimal controller that is used when we have a model (available) of the system being controlled. The goal of MPC is to minimize a predefined cost function while satisfying constraints such as system dynamics, actuator limitations, etc. At each time step, we calculate the best set of control actions that minimizes the cost function over a specific time horizon and pick the action for the most immediate time step — and the process repeats at the following time step. This is illustrated in the figure below.
While computationally expensive, MPC is much more sophisticated than traditional controllers such as PID or even iterative LQR as it can more effectively handle system latency, actuator constraints, as well as time variant system dynamics [1]. As an aside, if the system dynamics are linear and time invariant (i.e. LTI) and there are no actuation constraints, then MPC boils down to the classical LQR controller.
MPC Overview
As stated above, in MPC the objective is to minimize the cost function while satisfying system dynamics and actuator constraints. This is mathematically represented as follows:
Where x is the state, u is the control input/actuation, c is the cost function, and f is the system dynamics’ model. There are additional constraints such as: (1) the initial state (used for the optimization) is equal to the currently observed state and (2) actuation constraints as we cannot arbitrarily control the actuator — although this is not shown in the figure above.
While in the above figure the cost function and system constraints are computed through the end of time T (i.e. at each time-step we are re-planning the entire trajectory), this is not feasible for most practical situations as T can be very long. Instead, a more practical approach at each time step is to re-plan the trajectory out to a fixed time horizon H, so the cost summation and constraints go from k=t to k=t+H. For this reason, MPC is also know as receding horizon control.
Although we will dive into each of the below in greater detail, at a high level, the following steps are used for setting up an MPC controller — as per Udacity’s MPC lecture notes [4]:
- Depending upon the problem statement, set the horizon window by selecting the appropriate trajectory length (N) and time-step duration (dt).
- Using the reference trajectory way points (from the path planner), fit a polynomial curve, which is then used to compute the cross track and orientation errors.
- Using the problem statement again, select an appropriate vehicle dynamics model.
- Determine any physical constraints that must be obeyed, e.g. actuator limitations and other such limitations.
- Using the cross track and orientation errors, create an appropriate cost function for the MPC solver to minimize.
Upon building an appropriate vehicle dynamics model, cost function, and other parameters as outlined in the above five steps, we can now execute an MPC controller as follows:
- Set the MPC solver’s initial state to the vehicle’s current state.
- Run the optimization solver (Ipopt solver was used for this project). The solver returns a vector of control inputs at each time step (over the horizon window) that minimizes the cost function.
- Apply the first time-step’s control/actuation signals to the vehicle and discard the rest of the control inputs.
- Repeat the process (i.e. back to step 1)
Having seen an overview of how an MPC controller works, let us now dive deeper into each of the steps outlined above.
A. State-Space Representation & Vehicle Dynamics Model
Given MPC is a constrained optimization problem at every time step, having a good vehicle dynamics model is very important. But since the optimization problem is to be solved at every time point, the model cannot be very complicated due to the associated computational challenges. Hence, there is a tradeoff between model accuracy and computational speed. For this project, the model used is the basic kinematics model of the vehicle. It is a state-space based kinematics model with the state vector defined as s = [x, y, ψ, v], whereby:
- x is the position of the car
- y is the position of the car
- ψ is the orientation of the car
- v is the velocity/speed of the car
The simulator provides the state variables x, y, ψ, and v. The (x, y) position, which is in the map coordinate system, needs to be transformed into the vehicle coordinate system using translation followed by rotation.
Vehicle Actuators
The actuation signal is a vector [a, δ] where a is the throttle that controls acceleration/braking (negative throttle corresponds to braking) and δ is the steering angle that controls the vehicle orientation. These are computed by the MPC optimizer/solver and then sent to the simulator. The actuation signal is bounded by the following limits:
δ is in the range [-π/8, π/8]
a in the range [-1,1], i.e. between full brake and full throttle
State Update Equations
The state update equations are basic kinematic equations of motion used to set constraints on the optimization problem such that the optimizer takes the vehicle dynamics into account. They are first-order discrete-time difference-equations. The following dynamics model is used to compute the next state given the current one:
x’ = x + v*cos(ψ)*dt
y’ = y + v*sin(ψ)*dt
v’ = v + a*dt
ψ’ = ψ + (v/L_f)*δ*dt
(equations by author)
While the IPopt solver used in this project can handle these nonlinear constraints, other solvers may not be able to. In such cases where the MPC solver can’t handle nonlinear constraint equations, then at each time-step, they can be linearized (using Taylor series expansion) and re-written into the canonical state-space matrix form as s’ = As + Bu, where s is the state vector, u is the control vector, A is the matrix describing natural state transition, and B is the matrix describing control action’s effect on the state vector. Additionally, if the state is not fully observable, then we have the observation equation as o = Cs using the observation matrix C.
With that said however, in order for MPC to work well, we need to have full state observability. While for this project the state is indeed fully observable (i.e. the matrix C is just a 4x4 identity matrix), in most practical situations the state is not fully observable. In such cases we need to use a Bayes filter based state estimator (e.g. Kalman filter) to get the full state representation from partial (or noisy) state observations.
B. Cost Function
An important component of the MPC is its cost/error function — because that is what the optimizer minimizes. A well defined cost function is crucial for the optimizer to be effective, thus it needs to be properly tuned based upon the problem statement. The cost function used in this project is a quadratic function that is a weighted sum of the following quadratic terms at each time step — that are summed across the horizon window (which again is the number of time-steps we are forecasting into the future for):
- squared cross track error (cte) is the difference between the car’s position and the reference trajectory
- squared orientation error (ψ error i.e. epsi) is the difference between the car’s orientation and the desired/target orientation
- squared difference between current and reference speed
- squared value of the throttle and steering actuation (we want to minimize this as it influences the car’s energy consumption)
- squared value of the rate of change of throttle and steering actuation (for smooth driving)
cte and epsi are given large weights for accurate control. Furthermore, the rate of change of steering angle and throttle are also given large weights for a smooth trajectory.
The reference position used in computing cte is set to zero (i.e. corresponding to the middle of the track). The reference orientation used in computing epsi is also set to zero (i.e. the vehicle should be forward facing). The reference speed is set to 40 m/s. The horizon window is represented as N in the below code snippet. These error terms are multiplied by carefully chosen weights; and in the below code snippet, the cte weight is shown as wt1, epsi weight is shown as wt2, etc. Properly tuning of these weights (by experimenting with different values) is crucial for fast and smooth driving. Below is a code snippet showing how the total cost fg[0] is calculated.
In order to speedup the optimization process, the initial values of actuation (used by the MPC solver) is the same as the most recent set of actuation signals actually applied to the vehicle. This is much more realistic (and computationally faster) than random or zero initialization.
C. Horizon Window
The frequency (dt) and timestep length (N) are two of the important parameters used for tuning the MPC. Together they determine the horizon window over which optimization is to be performed.
Frequency (dt)
The time duration between two subsequent time-steps is represented as dt — as shown in the above state update equations. Inverse of dt is referred to as frequency in the MPC literature.
Through experimentation, it was observed that a dt of 110msec or below caused the car to oscillate about the center of the track —likely due to the fact that the actuator inputs are applied at a much faster rate than the vehicle’s ability to respond and so it is not able to keep up; and thus, it almost continuously tries to course correct itself.
On the contrary, using a large dt of 200msec and above, while the motion is smoother, the car rolls-off the track edges around curves — because now the actuator inputs are applied at a much slower rate compared to the rate of change of the road conditions (which is dependent upon vehicle speed). Optimal performance was obtained with a dt of about 145msec.
Time-step length (N)
This determines the number of time-steps the MPC controller plans in the future for. The higher this is, the further ahead the MPC controller plans for. But the downside of large N is that it requires a lot more computations, which can lead to latency induced inaccuracies as the solver may not be able to provide the solution in real-time. Additionally, with a large N, any model inaccuracies will cause erroneous actuation predictions for longer periods of time — hence compounding the effects of model inaccuracies.
However, on the other hand, in order to develop an optimal control policy, it is important to optimize over a longer time horizon in order to properly account for the current actuation’s effect on future vehicle states. Moreover, the higher the desired speed of the car, the longer the prediction horizon needs to be in order to obtain the best control actions and stability. Hence, there is a trade-off.
N was fine tuned after first finding the optimal value for dt. Once the dt value was set, a few different values for N were tried. A high N of 30 caused the car motion to become rather jerky and was computationally expensive. The optimal value of N seemed to be around 10.
D. Polynomial Fitting of the Path-Planner Waypoints
The path-planner module generates the reference (x,y) co-ordinates that are sent to the vehicle controller. These co-ordinates are in the map space, so they are first transformed to the vehicle’s co-ordinate system. Thereafter, a 3rd degree (cubic) polynomial is used to fit these (x,y) waypoints . This polynomial is then used to describe the reference trajectory; and thus, compute the cross track error (cte) at each time step over the horizon window when performing optimization. For best performance and robustness, the waypoints are not preprocessed; instead, a polynomial curve is fitted in real-time.
E. Hardware Latency
To realistically account for real-world hardware delays, the simulator has a built-in 100ms latency. As a result, the throttle and steering angle control signals sent to the simulator are actually applied to the vehicle after this delay. Unlike other controllers, MPC controllers are generally much better at handling latency due to the following two reasons:
- We can explicitly account for such delays in the state-update equations before passing the current vehicle state to the MPC solver. In other words, the initial state used by the MPC solver is generated by predicting the measured state forward in time (i.e. the latency time) using the kinematic model of the vehicle and assuming the previous set of actuation holds over the latency period. This means that the optimal control signals generated by the solver has already taken into consideration the true vehicle state when the actuation signals are actually applied.
- The frequency (dt) parameter can be set to be slightly larger than the latency — this way the state update equations will implicitly take latency into account.
Together with these two approaches, the MPC controller can handle latency of even hundreds of milli-seconds. Which is something very challenging (if not impossible) for traditional controllers like PID, LQR, etc.
Conclusion
MPC optimizes the car’s trajectory based upon its current state by computing various trajectories (i.e. steering angle and throttle actuations at each time-step across the horizon window) and their corresponding costs. The trajectory with the lowest cost is selected and the actuation vector corresponding to the first time-step is executed. And the process repeats at the next time-step.
Hence, MPC is much better than traditional controllers because it optimizes the vehicle’s actuation signals based upon its current state, its dynamics, the actuator constraints, and the reference trajectory from the path-planner. As a result, I was able to achieve a much higher drivable speed compared to the results of my PID controller or behavioral cloning projects. The vehicle never left the drivable portion of the track even while moving at a speed of over 80 MPH.
Again, for more details, please refer to my GitHub repository.
Future Experimentation
MPC + Deep Learning
As good as MPC is, it is important to also recognize its drawbacks. The major problem with MPC is the need for full optimization (over the control variables) at each time-step. Which is computationally expensive. I wonder if we can learn a policy network (i.e. neural network) using the system dynamics model and the above cost function (across a time horizon H) to predict the optimal control signal based upon the current state of the vehicle. This is mentioned in Yann LeCun’s lecture [3] on MPC at 1:03:00 and when he talks about systems I & II in the human mind at 1:55:00.
MPC + Path-Planner
Another thing I’d like to investigate in the future is to combine the path-planner with the MPC controller. This is because both are solving a similar optimization problem. In particular, the path-planner objective is to find the optimal (x,y) co-ordinates at different time-steps while (1) driving at a particular speed, (2) being in the middle of the track, and (3) avoiding obstacles. Whereas the MPC objective is to find the optimal control actions at different time-steps while (1) following the reference trajectory (generated by the path-planner) and (2) satisfying the vehicle dynamics and actuator constraints.
So it is possible to change the MPC objective by additionally including the path-planner objective inside it. That is to say, we can set the MPC objective to find the optimal control actions at different time-steps in order to (1) drive at a particular speed, (2) be in the middle of the track, (3) avoid obstacles, and (4) satisfy the vehicle dynamics and actuator constraints. We can do so by modifying the MPC cost function and constraint equations. So this is another thing I’d like to investigate in the future.
References
[1] CMU 10703: https://katefvision.github.io/katefSlides/RECITATIONtrajectoryoptimization_katef.pdf
[2] CS287: https://people.eecs.berkeley.edu/~pabbeel/cs287-fa15/slides/lecture8boptimization-for-optimal-control.pdf
[3] DS-GA1008: https://www.youtube.com/watch?v=Pgct8PKV7iw&feature=youtu.be
[4] CarND: https://www.udacity.com/course/self-driving-car-engineer-nanodegree--nd013